Вгадай, що це за теорема

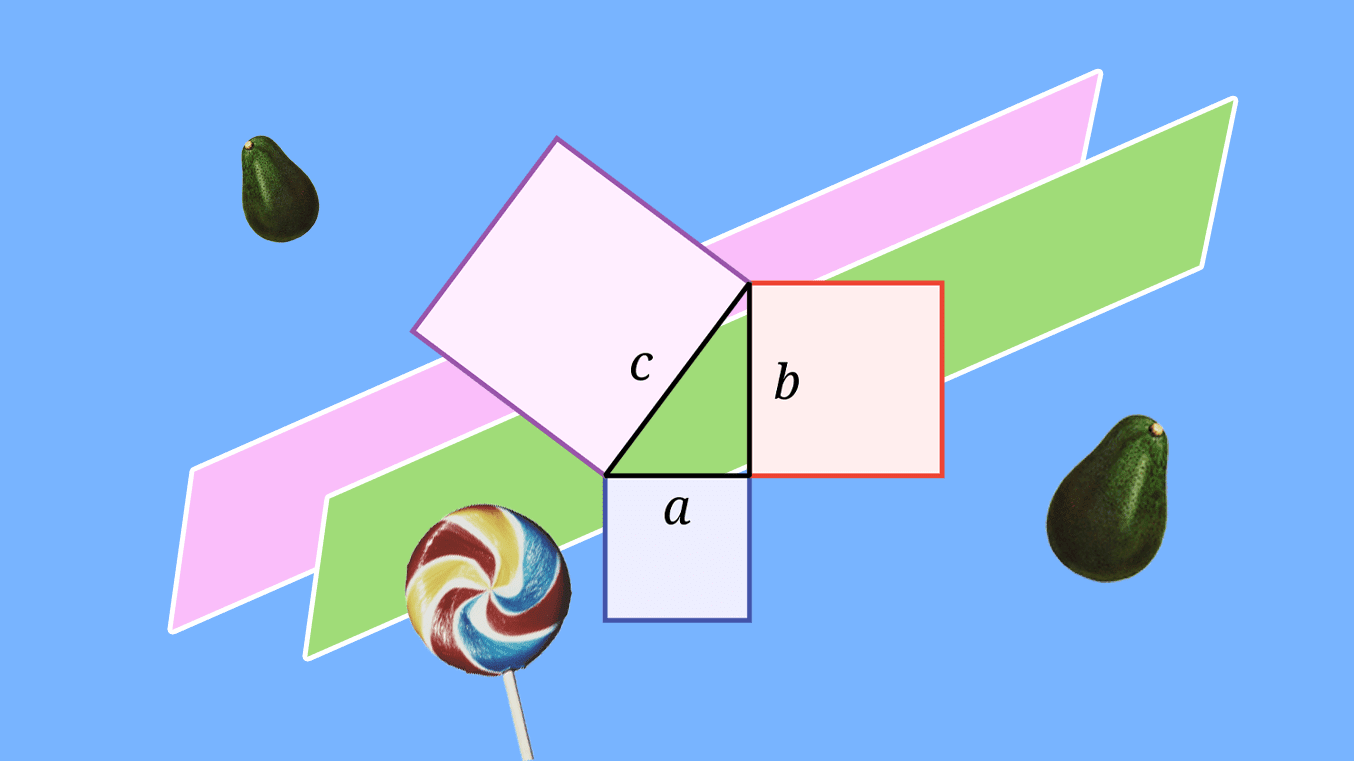
Це теорема Піфагора. Те, що у прямокутного трикутника квадрат гіпотенузи дорівнює сумі квадратів катетів, уперше довів цей грецький математик та філософ. Піфагор розглядав квадрат не як число, помножене саме на себе, а як квадрат, побудований на стороні трикутника.

Теорему для пошуку коренів зведеного квадратного рівняння вивів французький математик та астроном XVI століття Франсуа Вієт. Згідно з нею, сума коренів зведеного квадратного рівняння дорівнює другому коефіцієнту з протилежним знаком, а добуток коренів дорівнює вільному члену.

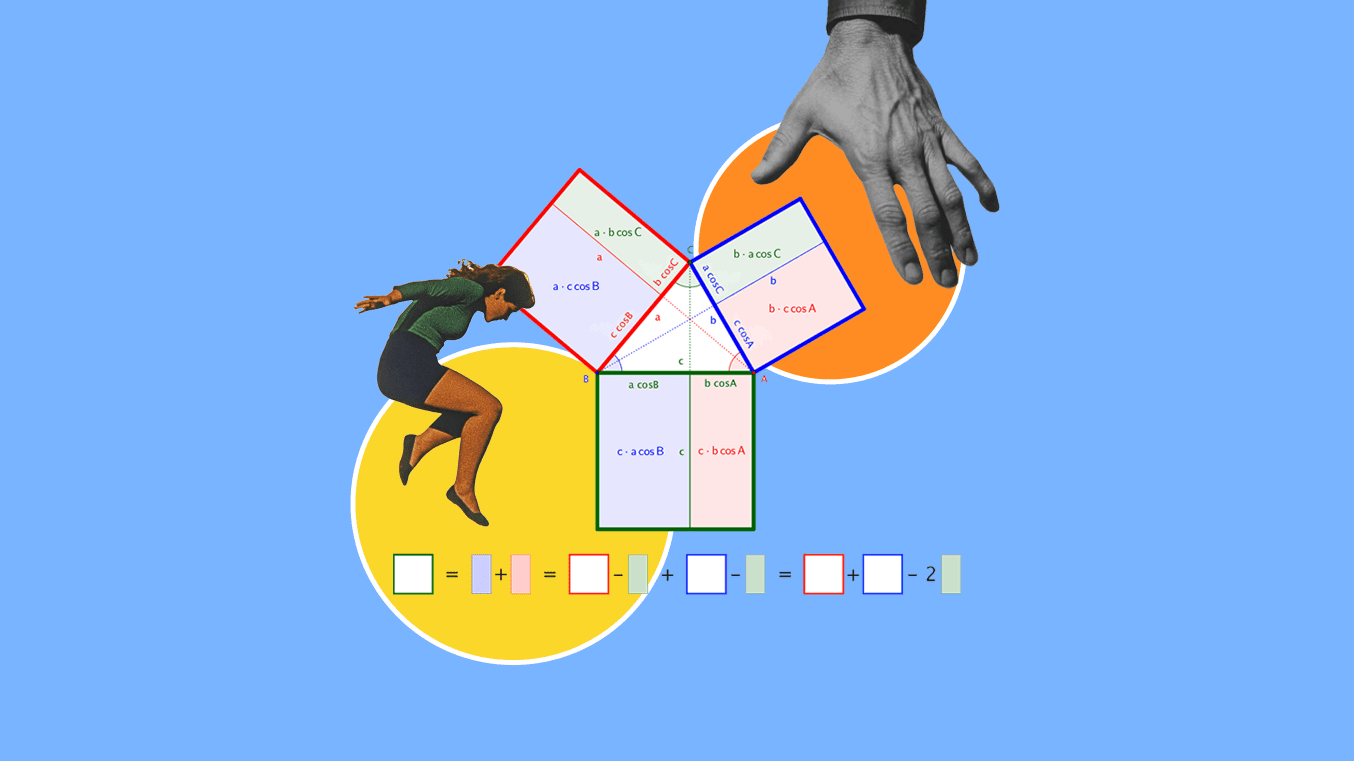
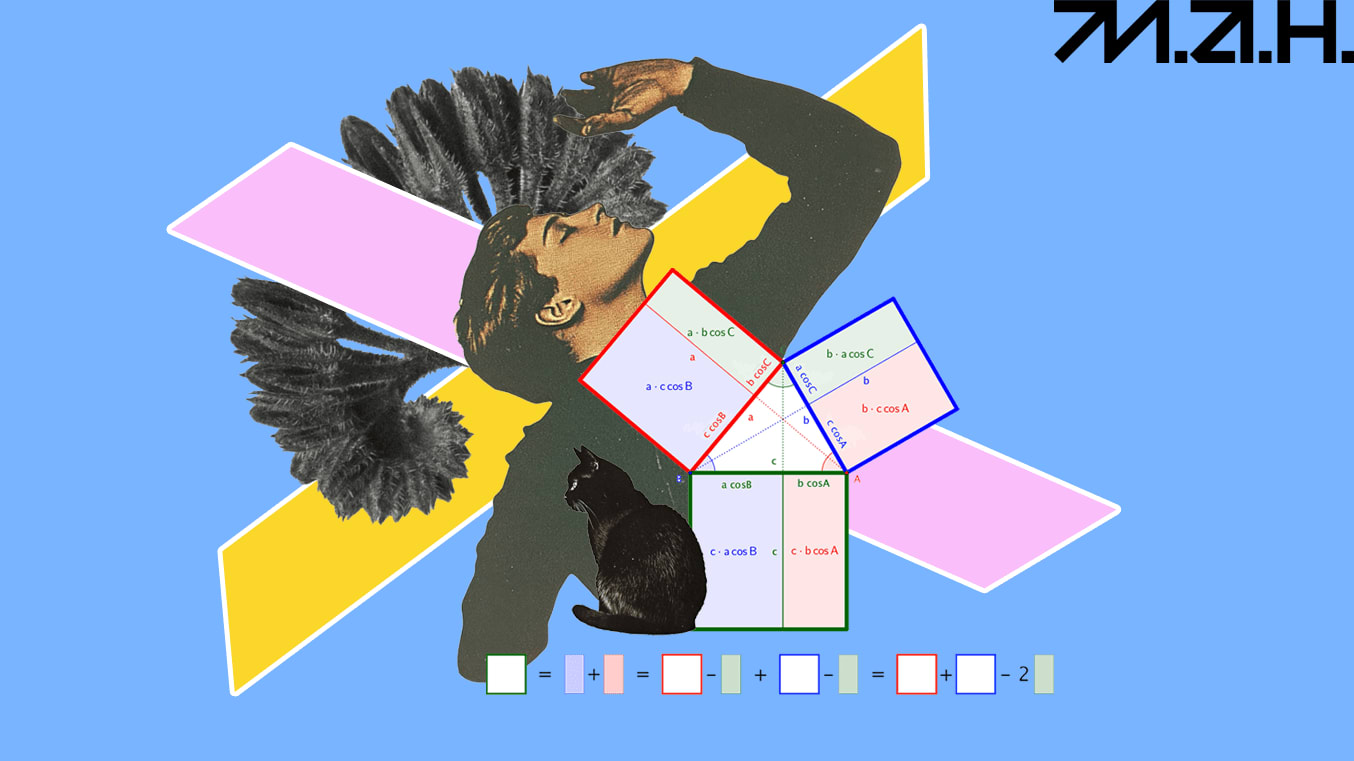
Теорема косинусів показує зв’язок довжини сторін трикутника з косинусом одного з кутів. Вона звучить так: квадрат сторони трикутника — це сума квадратів двох інших його сторін мінус подвоєний добуток цих сторін і косинуса кута між ними.

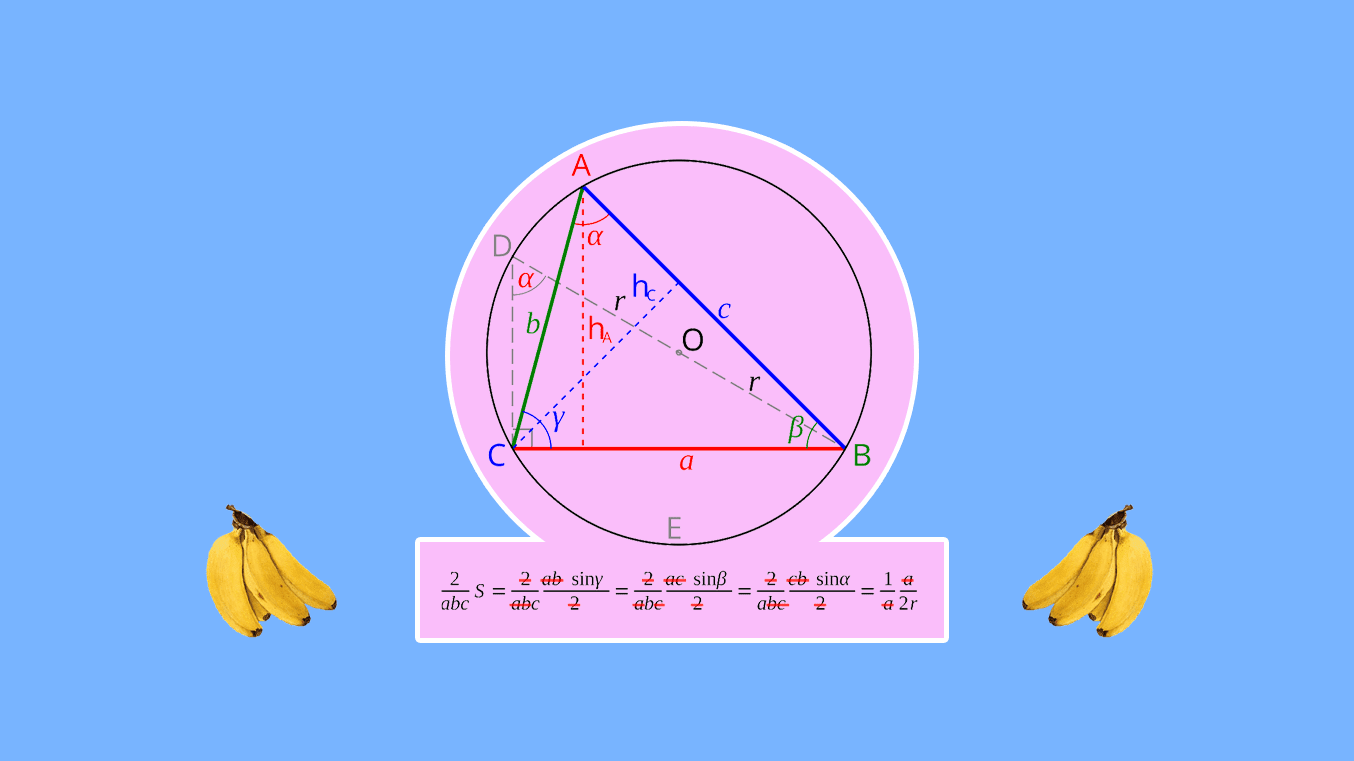
Це теорема синусів. Вона звучить так: відношення сторони трикутника до синуса протилежного кута дорівнює двом радіусам описаного кола.

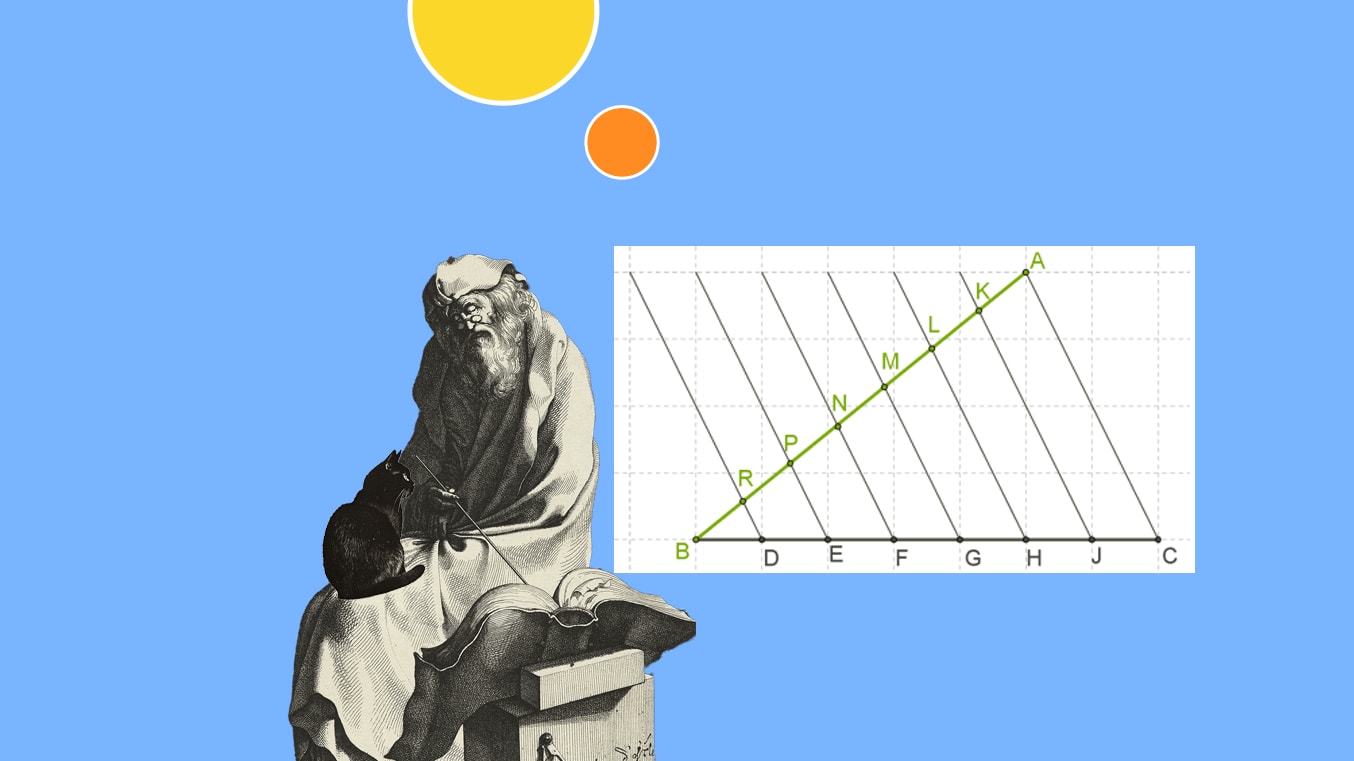
Фалес із Мілета — перший відомий грецький філософ і математик, що жив у VII–VI століттях до нашої ери. Науковець досліджував геометрію та використовував свої знання на практиці, як-от для вимірювання висоти пірамід. За теоремою Фалеса, якщо паралельні прямі перетинають прямі a i b, то відтинають на них пропорційні між собою відрізки.

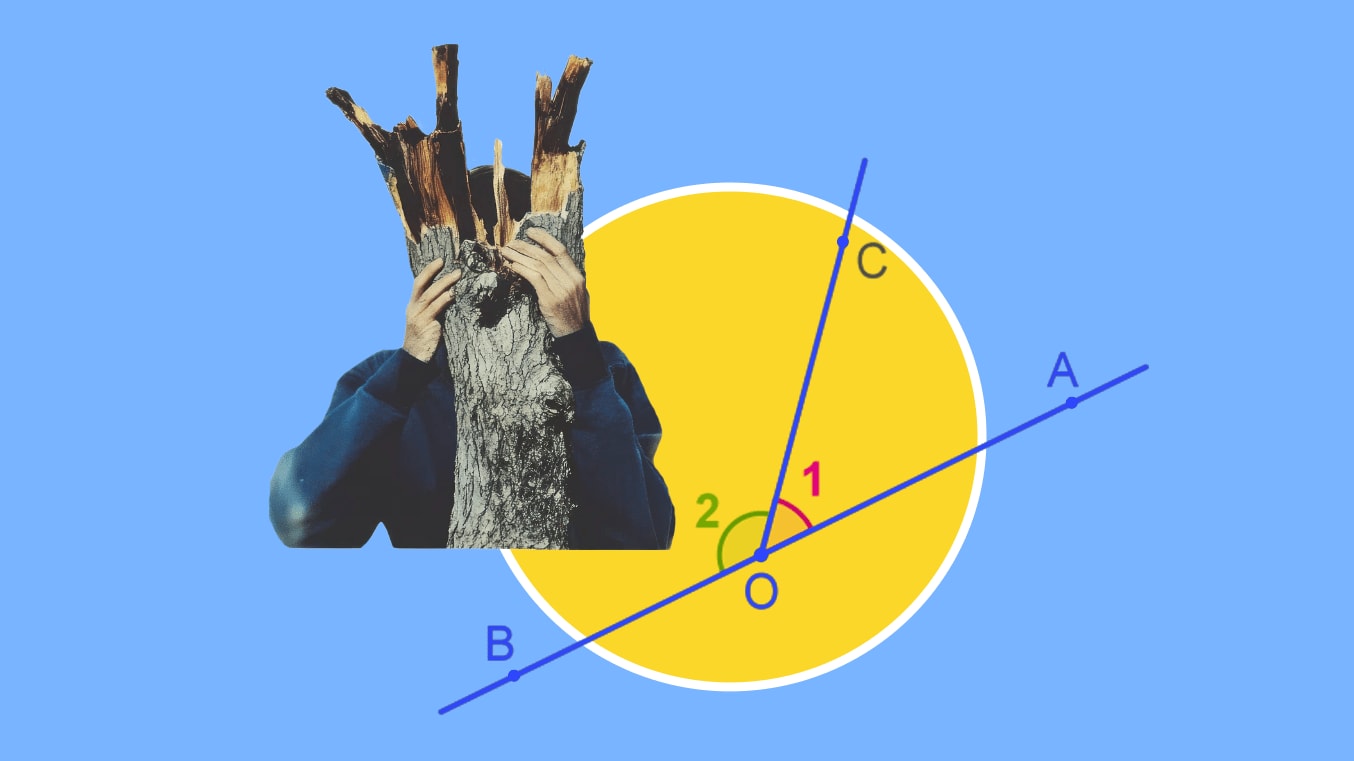
Теорема про суміжні кути стверджує: сума цих кутів становить 180 градусів.

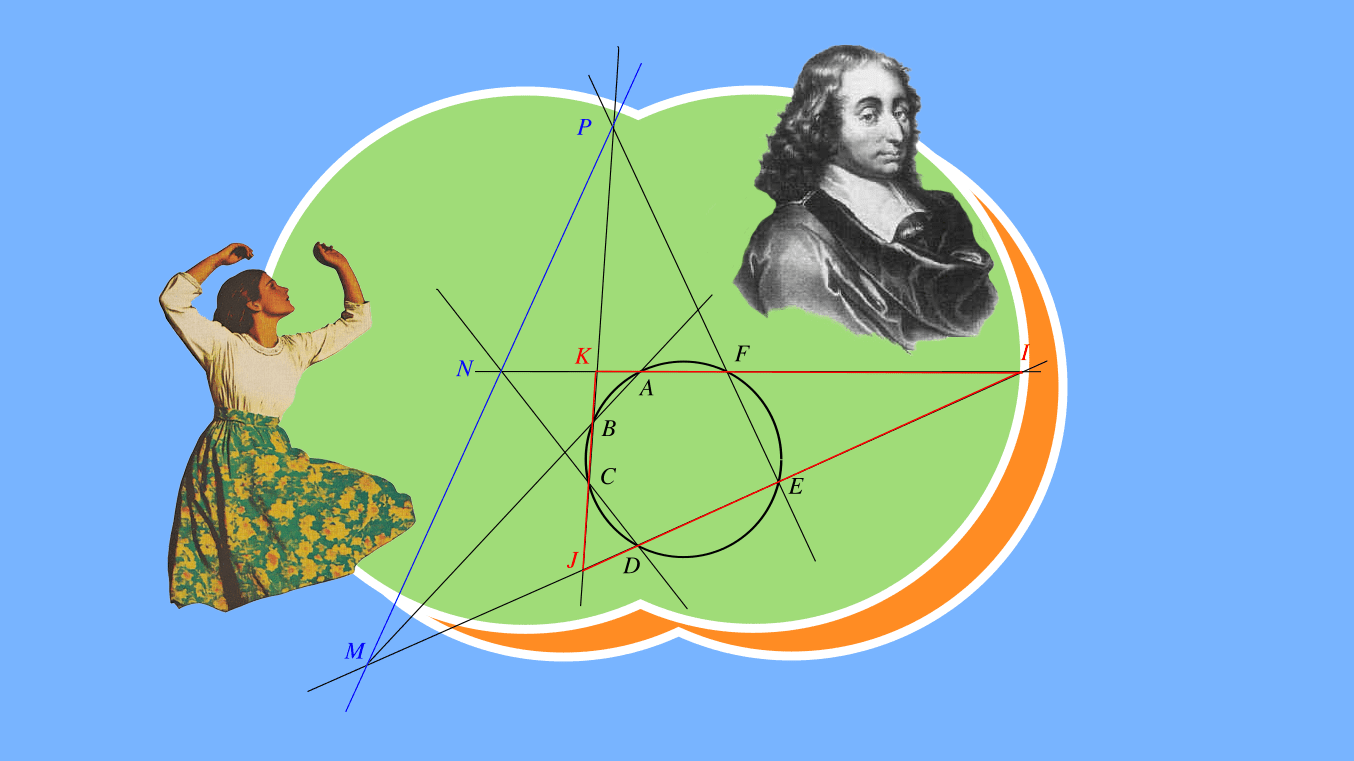
Це теорема Блеза Паскаля — французького математика і філософа XVII століття. Її разом з іншими геометричними відкриттями він розробив і представив у 16 років. Ця теорема стверджує: точки перетину продовження протилежних сторін шестикутника, вписаного у коло, лежать на одній прямій, яку ще називають прямою Паскаля.

Щоб дізнатися ймовірність появи однієї з двох несумісних подій, потрібно додати ймовірності кожної з них.